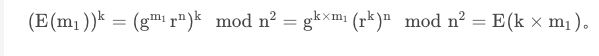fundamentals
- fundamental theorem of arighmetic
the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up to the order of the factors wiki - Euler’s totient function
In number theory, Euler’s totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as \( \phi (n) \), and may also be called Euler’s phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n. the collection of k is denoted by \( Z_{n}^{\ast } \), and \[ \phi(n) = |Z_n^{\ast }| \] - if p is prime, then \( Z_p^{\ast } = Z_p \), \( \phi(p) = p-1 \)
- if p is prime, for any integer r, then \( \begin{align} \tag{0.1} \phi(p^{r}) =p^{r-1}\phi(p)=p^{r-1}(p-1)\end{align} \)
- Euler’s totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime, then \(\phi(mn) = \phi(m)\phi(n)\)
- Euler’s product formula, it states
\[ \phi(n) = n \prod_{p|n}^{}(1-\frac{1}{p}) \]
where the product is over the distinct prime numbers dividing n. - Euler’s theorem
if \(a\) and \(n\) are coprime positive integers, and \( \phi(n)\) is Euler’s totient function, then \(a\) raised to the power \(\phi(n)\) is congruent to 1 modulo n; that is
\[a^{\phi(n)} \equiv 1 \bmod n\] - according to 7, we have \( a \cdot a^{\phi(n)-1} \equiv 1 \bmod n \). then
\[ a^{-1} = a^{\phi(n)-1} \] - Fermat’s little theorem
Fermat’s little theorem states that if p is a prime number, then for any integer a, the number
\(a^{p}-a \) is an integer multiple of p. In the notation of modular arithmetic, this is expressed as
\[ a^{p} \equiv a \bmod p\] - Binomial theorem
it states
\[ y = (1+n)^{x} = \sum_{k=0}^{x}\tbinom{x}{k}n^{k} = 1 + nx + \tbinom{x}{2}n^2 + …\]
observe that, the higher degree could be divided by \(n^2\). we have
\[ \begin{align} \tag{0.2} (1+n)^{x} \equiv 1 + nx \bmod n^2 \end{align} \]
therefore, \( y - 1 \equiv nx \bmod n^2 \). then we have
\[ x \equiv \frac{y-1}{n} \bmod n \].
In paillier, later we define \( \begin{align} \tag{0.3} L(y) = \frac{y-1}{n} \end{align} \)
therefore
\[ L(y \bmod n^2) \equiv x \bmod n \]
Paillier
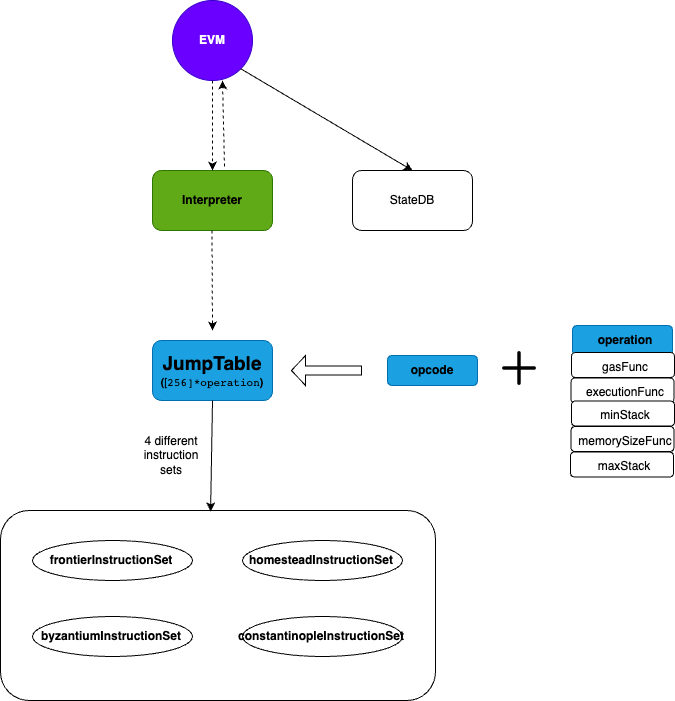
key generation
KeyGen() -> (pk, sk)
randomly select two big prime numbers \(p, q\). it shoud satisfy \(gcd(pq, (p-1)(q-1)) =1 \), \(p\) and \(q\) should have similar bit length. let \( n = pq \), \(\lambda = lcm(p-1, q-1)\). randomly sample \( g \in Z_{n^2}^{\ast}\). to simplify, let \( g = n+1\). we have
\[ pk=(n,g) \]
\[ sk = (\lambda)\]encryption
Enc(pk, m) -> c
randomly sample \( r \in Z_{n}^{\ast}\), then also have \( r \in Z_{n^2}^{\ast}\), cypher is calculated
\[ \begin{align} \tag{1.1} c = g^mr^n \bmod n^2 \end{align} \]Decryption
Dec(sk, c) -> m
Let \(L(x) = \frac{x-1}{n} \), we have message
\[ \begin{align} \tag{1.2} m = \frac{L(c^{\lambda} \bmod n^2)}{L(g^{\lambda} \bmod n^2)} \bmod n \end{align}\]proof of correctness
based on Eq(1), we have \[ \begin{align} \tag{1.3} c^{\lambda} \bmod n^2 = g^{m\lambda}r^{n\lambda} \bmod n^2 \end{align}\]
where \( r^{n\lambda} \bmod n^2 \equiv 1 \bmod n^2\), which is proved by Carmichael theorem later on. then Eq(3) becomes
\[ \begin{align} \tag{1.4} c^{\lambda} \bmod n^2 = g^{m\lambda}\bmod n^2 \end{align}\]
since \( g = n+1\), we have
\[ \begin{align} \tag{1.5} c^{\lambda} \bmod n^2 = (1+n)^{m\lambda}\bmod n^2 \end{align}\]
According to Eq(0.2), we have
\[ \begin{align} \tag{1.6} c^{\lambda} \bmod n^2 = 1 + nm\lambda \bmod n^2 \end{align}\]
\[ \begin{align} \tag{1.7} g^{\lambda} \bmod n^2 \equiv (1+n)^{\lambda} \bmod n^2 = 1 +\lambda n \bmod n^2 \end{align}\]
therefore, based on definition given by Eq(0.3) we have
\[ \begin{align} \tag{1.8} L(c^{\lambda} \bmod n^2) = \frac{c^{\lambda}-1}{n} \bmod n^2 \end{align} \]
Substitute Eq(1.6) into Eq(1.8), we have
\[ \begin{align} \tag{1.9} L(c^{\lambda} \bmod n^2) = m\lambda \bmod n^2 \end{align} \]
Further, we have
\[ \begin{align} \tag{1.10} L(g^{\lambda} \bmod n^2) = \frac{g^\lambda -1}{n} \end{align} \]
Sub Eq(1.7) into Eq(1.10), we have
\[ \begin{align} \tag{1.11} L(g^{\lambda} \bmod n^2) = \frac{\lambda n}{n} \equiv \lambda \bmod n^2\end{align} \]
At last, Eq(1.2) becomes (bu sub Eq1.9 and Eq1.11)
\[ \begin{align} m = \frac{L(c^{\lambda} \bmod n^2)}{L(g^{\lambda} \bmod n^2)} \bmod n = \frac{m \lambda}{\lambda} \equiv m \bmod n \end{align}\]
proved!!!Carmichael theorem
In number theory, a branch of mathematics, the Carmichael function \(λ(n)\) of a positive integer n is the smallest positive integer m such that \(a^{m}\equiv 1{\pmod {n}}\) (similar but different from Euler’s totient function). Carmichael’s λ function, the reduced totient function, and the least universal exponent function

let \( n = pq\), where p and q are prime numbers; \( \phi(n)\) is the Euler’s totient function. Let \(\lambda(n)\) denotes carmichael function. We have \(\phi(n)=(p-1)(q-1)\) and \( \lambda(n)=\phi(n) = (p-1)(q-1)\).
Since \( |Z_{n^2}^{\ast}| = \phi(n^2) = n \phi(n)\) (according to Eq(0.1)). Thereby, for any \( w \in Z_{n^2}^{\ast}\)
\[ \begin{align} \tag{1.12} w^{n\phi(n)} \equiv w^{n\lambda} \equiv 1 \bmod n^2 \end{align}\]
\[ \begin{align} \tag{1.13} w^{\lambda} \equiv 1 \bmod n \end{align}\]
Eq(1.13) is just Carmichael’s function
Based on Carmichael’s theorem
\[ \lambda(n^2) = lcm(\lambda(q^2),\lambda(p^2)) = lcm(\phi(q^2),\phi(p^2)) = lcm(q(q-1), p(p-1)) = pq(lcm(p-1, q-1)) = n\lambda(n) \]
therefore, we have
\[w^{\lambda(n^2)} = w ^{n\lambda} \equiv 1 \bmod n^2\]
Addition homomorphic
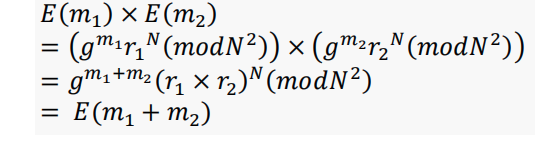
Multiplication homomorphic