introduction
PLONK, standing for the unwieldy quasi-backronym “Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”. PLONK still requires a “universal and updateable” trusted setup, meaning each program share the same setup. Secondly, there is a way for multiple parties to participate in the trusted setup such that it is secure as long as any one of them is honest.
preliminary
observation 1
a key fact: for non-zero \( f \in \mathbb{F_p}^{\le d}[X]\)
for \( r \leftarrow \mathbb{F_p}: Pr[f(r) = 0] \le d/p\)
understanding: polynomial \(f\) contains at most \(d\) roots of zeros.
suppose \( p \approx 2^{256}\) and \( d \approx 2^{40}\) then \(d/p\) is negligible.
Therefore, for random \( r \leftarrow \mathbb{F_p}\) if \(f(r) = 0\) then \(f\) is identically zero w.h.p (with high probability)
=> a simple zero test for a committed polynomial
Note SZDL lemma: this also holds for multivariate polynomials (where d is total degree of f)
observation 2
let \(f,g \in \mathbb{F_p}^{\le d}[X]\).
for \( r \leftarrow \mathbb{F_p}\), if \(f(r) = g(r)\), then \(f = g\) w.h.p
\(f(r)-g(r)=0\) => \(f-g=0\) w.h.p
=> a simple equality test for two committed polynomials
useful proof gadgets
1. zero test
let \( \omega \in \mathbb{F_p} \) be a primitive k-th root of unity \(( \omega ^{k} = 1)\)
set \( H:= \{1,\omega,\omega^2,\omega^3,…,\omega^{k-1}\} \subseteq \mathbb{F_p} \)
let \( f \in \mathbb{F_p}^{\le d}[X]\) and \( b, c \in \mathbb{F_p}\) \((d \ge k)\)
task: prove that \(f\) is identically zero on \(H\)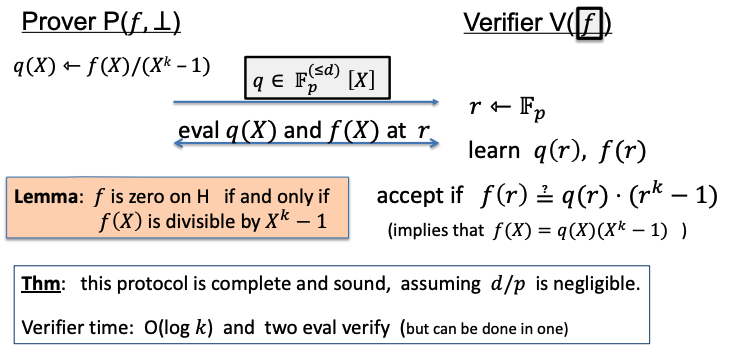
info the box of \(f\) means the commitment of polynomial \(f\), i.e \(com_f\)
2. product check
product check on \(\Omega: \quad \prod_{a\in \Omega} f(a) = 1\)
Set \( t \in \mathbb{F_p}^{\le k}[X]\) to be the degree-k polynomial:
\[ t(1) = f(\omega^0) = f(1), \quad t(\omega^s) = \prod_{i=0}^{s}f(\omega^{i}) \quad for \quad s = 1,…, k-1\]
Then
\(t(\omega) = f(1) \cdot f(\omega), \quad t(\omega^2) = f(1) \cdot f(\omega) \cdot f(\omega^2), … \)
\(t( \omega^{k-1}) = \prod_{a \in \Omega}f(a) = 1\)
and \( t(\omega \cdot x) = t(x) \cdot f(\omega \cdot x) \) for all \(x \in \Omega \) (including at \(x = \omega^{k-1}\))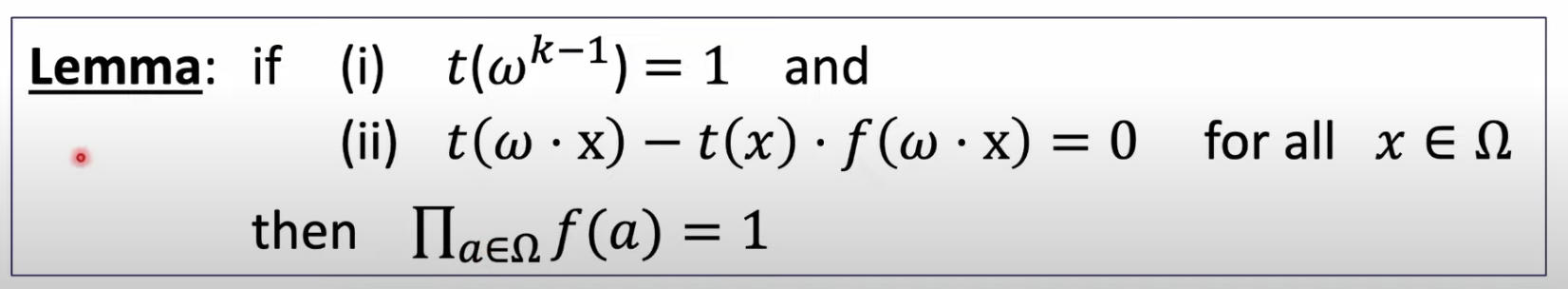

Same works for rational functions: \( \prod_{a \in \Omega}{f/g}(a) =1 \)
The proof is similar
3. permutation check
let \(f,g\) be polynomials in \(\mathbb{F_p}^{\le d}[X]\). Verifier has \(com_f, com_g\).
Prover wants to prove that \((f(1),f(\omega^1),f(\omega^2),…,f(\omega^{k-1})) \in \mathbb{F_p}^{\le k}[X]\) is a permutaion of \((g(1),g(\omega^1),g(\omega^2),…,g(\omega^{k-1})) \in \mathbb{F_p}^{\le k}[X]\)
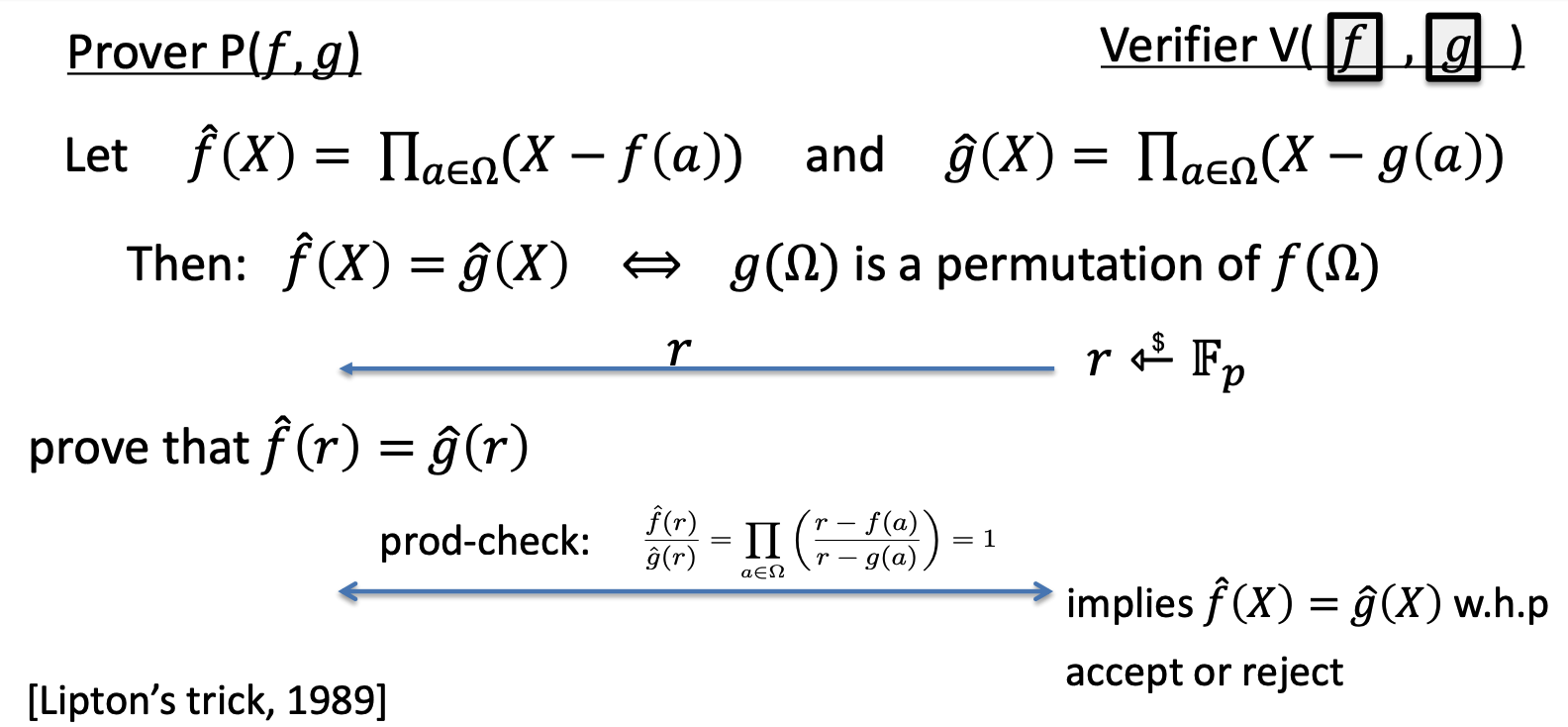
4. prescribed permutation check





PLONK: a poly-IOP for a general circuit C(x,w)
step 1: compile circuit to a computation trace (gate fan-in = 2)
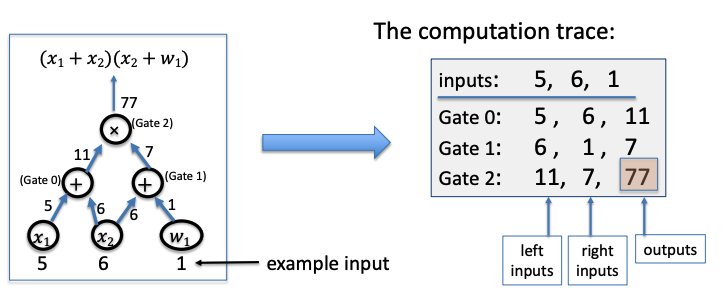
and encode the trace as polynomial
let \(|C|\) be the total number of gates, \(|I| := |I_x| + |I_w|\) be total number of inputs, where \(|I_x|\) is the number of public inputs, \(I_w\) is the number of private inputs.
Let \(d=3*|C|+|I|\) and \( \Omega=\{1,\omega,\omega^2,\omega^3,…,\omega^{d-1}\} \)
prover interpolates \( T \in \mathbb{F_p}^{\le d}[X]\) such that
- T encodes all inputs: \( T(\omega^{-j}) \)= input #j, for j = 1,…,|I|
- T encodes all wires:
\(LeftInput=f(\omega^{3l})\), \( RightInput=f(\omega^{3l+1})\), \(Output=f(\omega^{3l+2})\), for \(l = 0,1,…, |C| -1\)
For the example,
inputs
\(x_1= 5 = T(\omega^9)\), \(x_2= 6 = T(\omega^{10})\), and \(w_1 = 1=T(\omega^{11})\)
wires
\(5=T(\omega^0)\), \(6=T(\omega^{1})\), and \(11=T(\omega^{2})\)
\(6=T(\omega^3)\), \(1=T(\omega^{4})\), and \(7=T(\omega^{5})\)
\(11=T(\omega^6)\), \(7=T(\omega^{7})\), and \(77=T(\omega^{8})\)
step 2: proving validity of T
Prover needs to prove 4 things
- \(T(x)\) encodes the correct public inputs
Both prover and verifier interpolate a polynomial \( v(x) \in \mathbb{F_p}^{\le |I_x|}[X]\)
that encodes the \(x\)-inputs to the circuit:
\(v(\omega^{-j}) =\) input #j, for \(j = 1, …, |I_x|\)
In our example, \(v(\omega^{-1} = 5), v(\omega^{-2} = 6)\)
Let \( \Omega_{inp}=\{\omega^{-1},\omega^{-2},…,\omega^{-|I_x|}\} \)
Prover proves by using a ZeroTest on \(\Omega_inp\) to prove that
\[T(y) - v(y) =0 \quad \forall y \in \Omega_{inp}\] - every gate is evaluated correctly
Idea encode gate types using a selector polynomial \(S(X)\)
define \(S(X) \in \mathbb{F_p}^{\le d}[X]\) such that \( \forall l = 0, …, |C| -1\):
- \(S(\omega^{3l}) =1\) if gate #l is an addition gate
- \(S(\omega^{3l}) =0\) if gate #l is a multiplication gate
Then, \( \forall y \in \Omega_{gates} : = \{1,\omega^{3},\omega^{6},…,\omega^{3(|C|-1)}\} \)
\(S(y) \cdot [T(y) + T(\omega y)] + (1-S(y))\cdot T(y) \cdot T(\omega y) = T(\omega^2 y)\)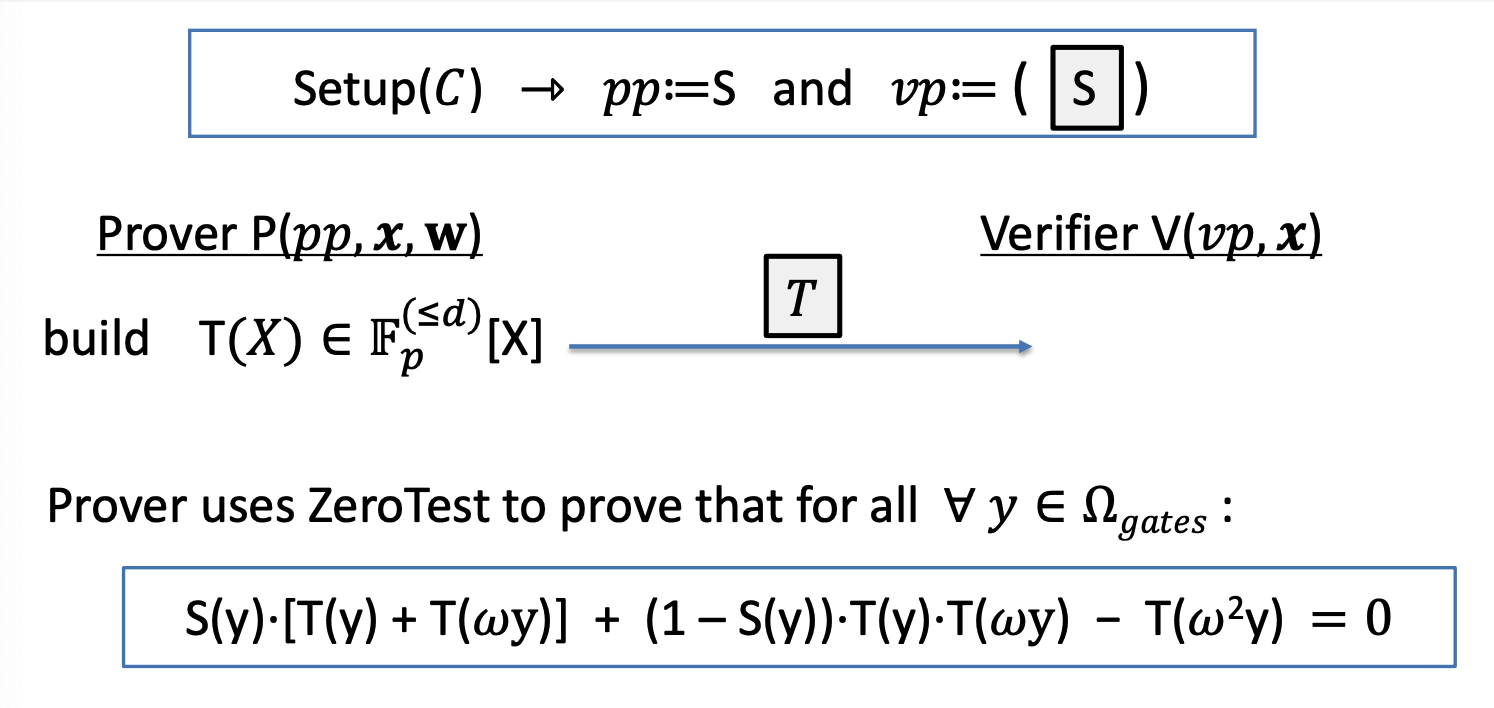
- the wiring is implemented correctly (coppy constraint)

\(T(\omega^9,\omega^0)=\sigma(\omega^0,\omega^9)\)
\(T(\omega^{10},\omega^1,\omega^3)=\sigma(\omega^1,\omega^3,\omega^{10})\)
\(T(\omega^2,\omega^6)=\sigma(\omega^6,\omega^2)\)
\(T(\omega^{11},\omega^4)=\sigma(\omega^4,\omega^{11})\)
\(T(\omega^{5},\omega^7)=\sigma(\omega^7,\omega^{5})\)
note: 9 is actually -1, 10 is -2, 11 is -3
Define a polynomial \(W: \Omega -> \Omega\) that implemnets a rotation
\( W(\omega^{10}, \omega^1, \omega^3) =(\omega^1, \omega^3, \omega^{10}) \), \(W(\omega^{9}, \omega^0)=(\omega^0, \omega^{9})\), …
Lemma: \(\forall y \in \Omega: T(y) = T(W(y))\) => wire constraints are satisfied
This could be proved using a prescribed permutation check
- the output of last gate is 0
this is to prove \(T(\omega^8) -77 = 0\)
custom gate

\(u, v, w, t, r\) are polynomials represent input variables (row number is the gate number). in the Add, Mul only circuits, there are only two inputs, namely LeftInput and RightInput. Hoever, here there are multiple inputs for custom gate.
In the above example, it is a constraint for \( v_4 + w_3 \cdot t_3 - t_4 = 0 \)
plonkup
plonkup is to ensure some values are in a pre-defined list. for example
| x1 | x2 | x3 | Output |
|---|---|---|---|
| \(a_{1,1}\) | \(a_{1,2}\) | \(a_{1,3}\) | \(a_{1,4}\) |
| \(a_{2,1}\) | \(a_{2,2}\) | \(a_{2,3}\) | \(a_{2,4}\) |
| … | … | … | … |
| \(a_{n,1}\) | \(a_{n,2}\) | \(a_{n,3}\) | \(a_{n,4}\) |
\(n\) is gate number. the task is to prove a vector