elliptic curve definition
for cryptographic use, we need to conside the curve not over the real numbers but over a finite field. the most popular fields GF(p), where all arithmetic is performed modulo a prime p.
the elliptic curve over \( Z_{p}, p>3 \), is the set of all pairs \( (x,y) \in Z_{p} \) which fulfill
\[ y^2 \equiv x^3 + a \cdot x + b \bmod p \]
together with an imaginary point of infinity \( \mathcal{O} \), where
\[ a,b \in Z_{p} \]
and the condition \( 4 \cdot a^3 + 27 \cdot b^2 \neq 0 \bmod p \)
the definition of elliptic curve requires that the curve is nonsingular. Geometrically speaking, this means that the plot has no self-intersections or vertices, which is achieved if the discriminant of the curve \( -16(4a^3) + 27b^2 \) is nonzero.
operations on elliptic curve
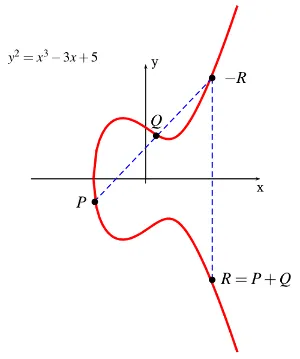
let’s denote the group operation with the addition symbol +. “addition” means that given two points and their coordinates, say \( P = (x_1, y_1) \) and \( Q = (x_2, y_2) \), we have to compute the coordidnate of a third point \( R (x_3, y_3) \). the construction works as follows: draw a line through P and Q and obtain a third point of intersection between the elliptic curve and the line (-R). Mirror this third intersection point along the x-axis. this mirored point is, by definition, the point R. point doubling (P+P = 2P) is a tangent line through the point P, and the rest is same.
the fomulae for Point Addition (P+Q) and Point Doubling (2P) is as below
\[ x_3 = s^2 - x_1 -x_2 \bmod p \]
\[ y_3 = s(x_1 - x_3) - y_1 \bmod p\]
where
\begin{equation}
s =
\begin{cases}
\frac{y_2-y_1}{x_2-x_1} \bmod p & if P \neq Q (\text{point addition}) \cr
\frac{3x_{1}^{2} + a}{2y_1} \bmod p & if P =Q (\text{point doubling})
\end{cases}
\end{equation}
note that the parameter s is the slope of the line through P and Q in the case of point addition, or the slope of the tangent through P in the case of point doubling.
Furthmore, we define an abstract point at infinity as the neutral element \( \mathcal{O} \).
\[ P + \mathcal{O} = P\]
according the group definition, we can now also define the inverse -P of any group element P as
\[ P + (-P) = \mathcal{O}\]
Therefore, the inverse of \( P = (x_p, y_p) \) is just \( P = (x_p, -y_p)\). since \( -y_p \equiv p - y_p\), hence
\[ -P = (x_p, p-y_p) \]
DLP(discrete log problem) with Elliptic curve
to set up DL cryptosystems it is important to know the order of the group.
Hasse’s theorem
given an elliptic curve E modulo p, the number of points on the curve is denoted by #E and is bounded by:
\[ p+1-2\sqrt{p} \leq \#E \leq p+1+2\sqrt{p} \]
Elliptic Curved Discrete Logarithm Problem (ECDLP)
Given an elliptic curve E. We consider a primitive elemnt P and another element T. The DL problem is finding the integer d, where \( 1 \leq d \leq \#E \), such that:
\[ P + P + ….+ P = dP = T \]
In cryptosystems, d is the private key which is an integer, while the public key T is a point on the curve with coordinates \( T = (x_T, y_T)\)
Usually a square-and-multiply algorithm is used to calculate point multiplication (the algorithm detail is not coverred in this post).