overview
this post is my reading summary of paper Yehuda Lindell 2017: Fast secure two-party ecdsa signing. the implementation could be found in tss-lib (golang), zengo’s library (rust).
Unlike other schemes like RSA, Schnorr signatures and more, it is particularly hard to construct efficient threshold signature protocols for ECDSA as there is an inverse computaion of \( k \).
In this paper, we consider the specific case of two parties (and thus no honest majority) and construct a protocol that is approximately two orders of magnitude faster than the previous best.
Comparing ECDSA signing to EC-Schnorr signing
In both cases, the public verification key is an elliptic curve point \( Q \) and the private signing key is \( x \) such that \( Q = x \cdot G \), where \( G \) is the generator point of an EC group of order \( q \).
Observe that Schnorr signing can be easily distributed since the private key \( x \) and the value k are both used in a linear equation. In contrast, in ECDSA signing, the equation for computing \( s \) includes \( k^{-1} \). Now, given shares \(k_1\), \(k_2\) such that \(k_1 + k_2 = k \bmod q\) .It is very difficult to compute \(k_1^{\prime}\), \(k_2^{\prime}\) such that \(k_1^{\prime} + k_2^{\prime} = k^{-1} \bmod q\)
two-party protocols for ECDSA signing use multiplicative sharing of \( x \) and of \( k \). That is, the parties hold \(x_1\), \(x_2\) such that \(x_1 \cdot x_2 = x \bmod q\), and in each signing operation they generate \(k_1\), \(k_2\) such that \(k_1 \cdot k_2 = k \bmod q\). This enables them to easily compute \(k^{-1}\) since each party can locally compute \(k_i^{\prime} = k_i^{-1} \bmod q\), and then \(k_1^{\prime}\), \(k_2^{\prime}\) are multiplicative shares of \(k^{-1}\). The parties can then use additively homomorphic encryption – specifically Paillier encryption – in order to combine their equations. For example, \(P_1\) can compute \(c_1 = Enc_{pk}(k_1^{-1} \cdot H(m))\) and \(c_2 = Enc_{pk}(k_1^{-1} \cdot x_1 \cdot r)\) . Then, using scar multiplication (denoted ⊙) and homomorphic addition (denoted ⊕), \( P_2 \) can compute \( (k_2^{-1} ⊙ c_1 ) ⊕ [( k_2^{-1} \cdot x_2) ⊙ c_2 ]\), which will be an encryption of
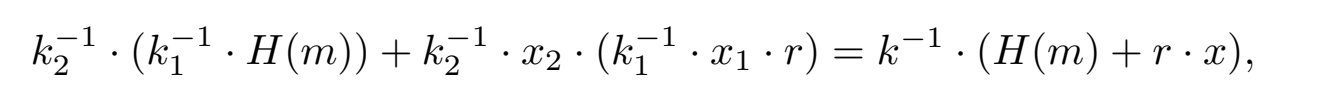
However, proving that each party worked correctly is extremely difficult. For example, the first party must prove that the Paillier encryption includes \(k_1^{-1}\) when the second party only has \(R_1 = k_1 \cdot G\). it must prove that the Paillier encryptions are to values in the expected range, and more. This can be done, but it results in a protocol that is very expensive.
their results
[WIP]